Engineering Analysis with ANSYS Software

Sign up for access to the world's latest research
Abstract
You may also complete your request on-line via the Elsevier homepage (http://www.elsevier.com), by selecting 'Customer Support' and then 'Obtaining Permissions'



















![where a is the angle between the normal vector n and the x-axis. For free surface:
where no forces are applied, t; = 0 and ty = 0.
where ¢,; and tf; are the x- and the y-components of the traction force t*, respectively,
while the bar over ¢; and t, indicates that those quantities are prescribed on that
portion of the surface. Taking n= [cosa, sina] as the outward unit normal vector
at a point of a small element of the surface portion S,, the Cauchy relations which
represent the equilibrium conditions for surface traction forces and internal stresses
are given by the following equations:](https://figures.academia-assets.com/48977193/figure_019.jpg)






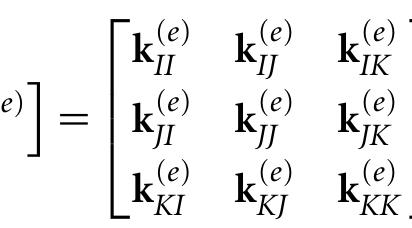




![Hence, from Equation (1.85), the element stiffness matrix for Element 1 [k©] is
calculated as](https://figures.academia-assets.com/48977193/figure_030.jpg)




















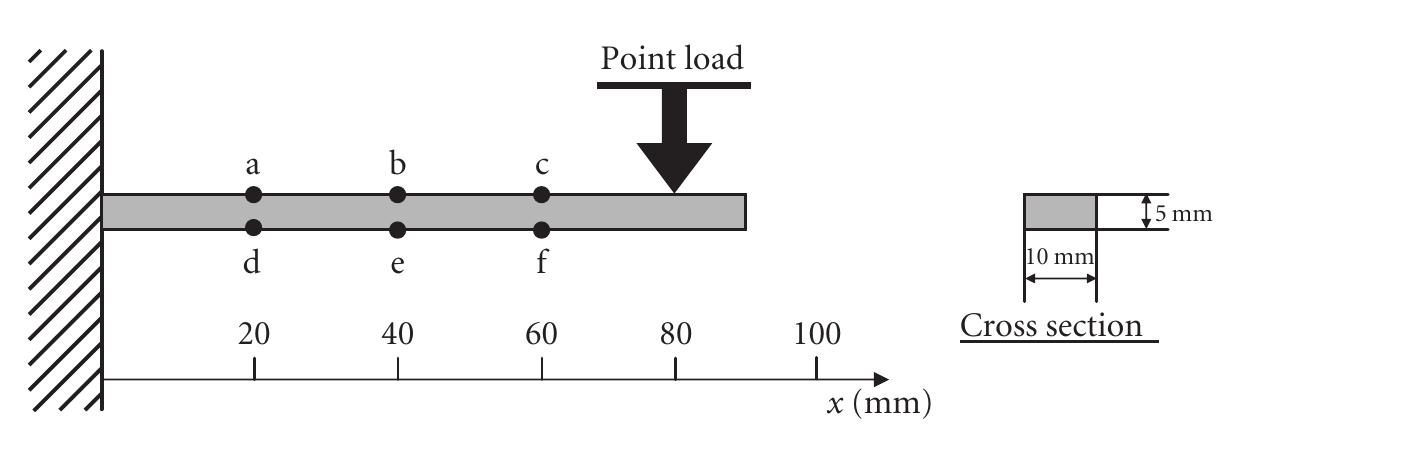




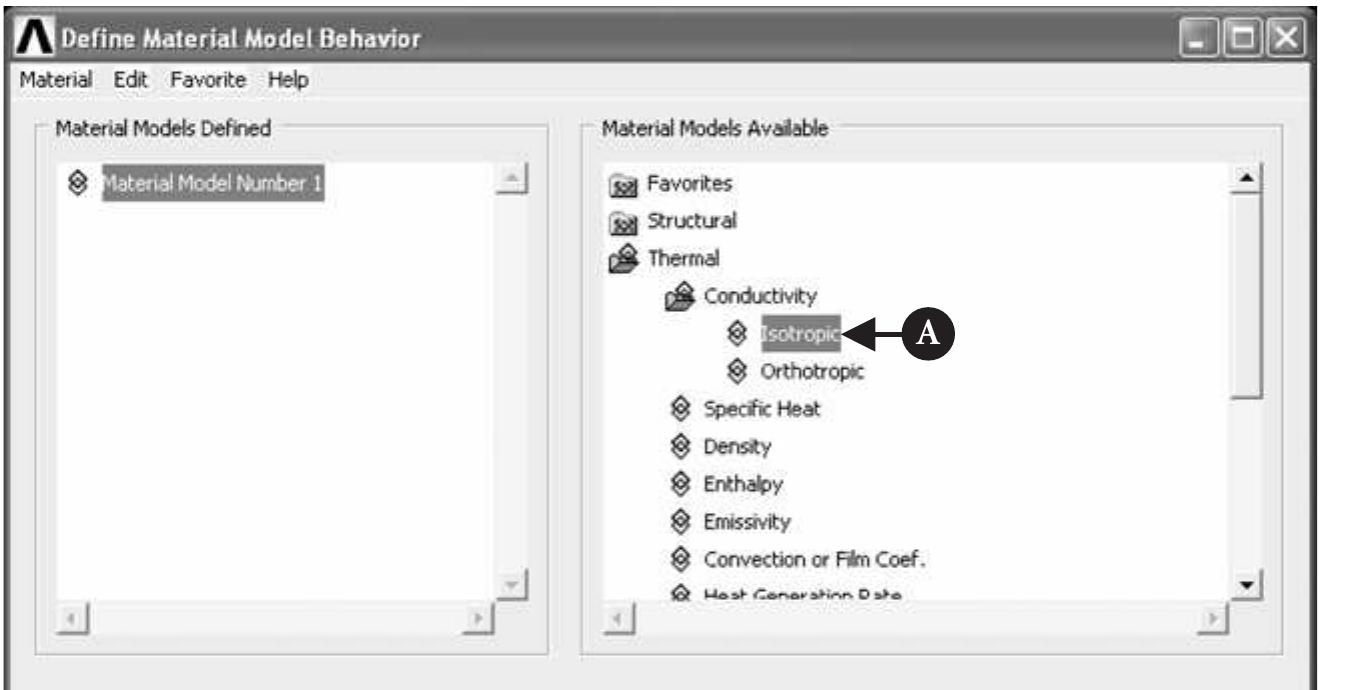
![Figure 3.8
Then the Define Material Model Behavior window opens as shown in
Figure 3.8:
(1) Double-click [A] Structural, Linear, Elastic, and Isotropic buttons one afte
another.](https://figures.academia-assets.com/48977193/figure_055.jpg)























































































































































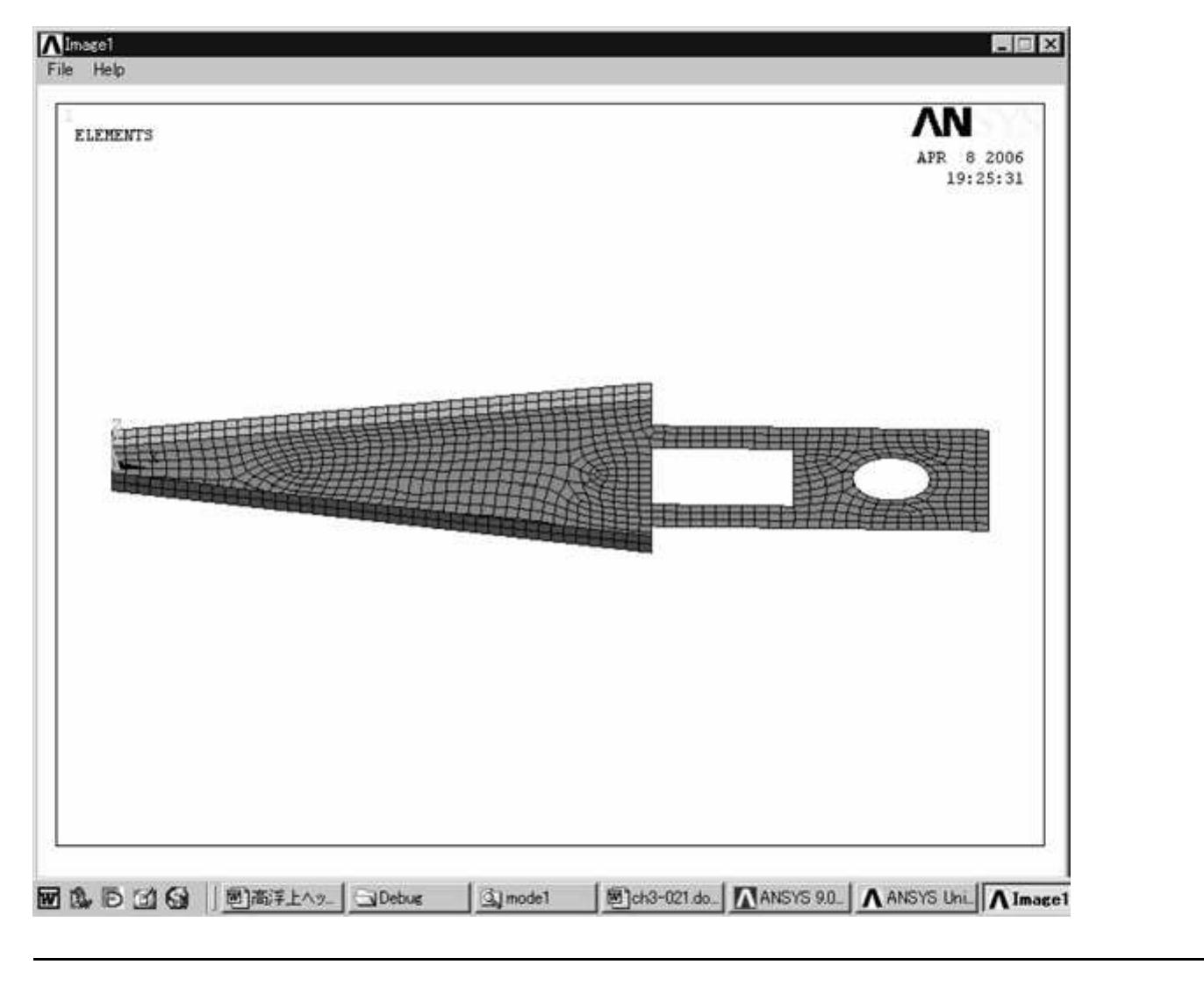










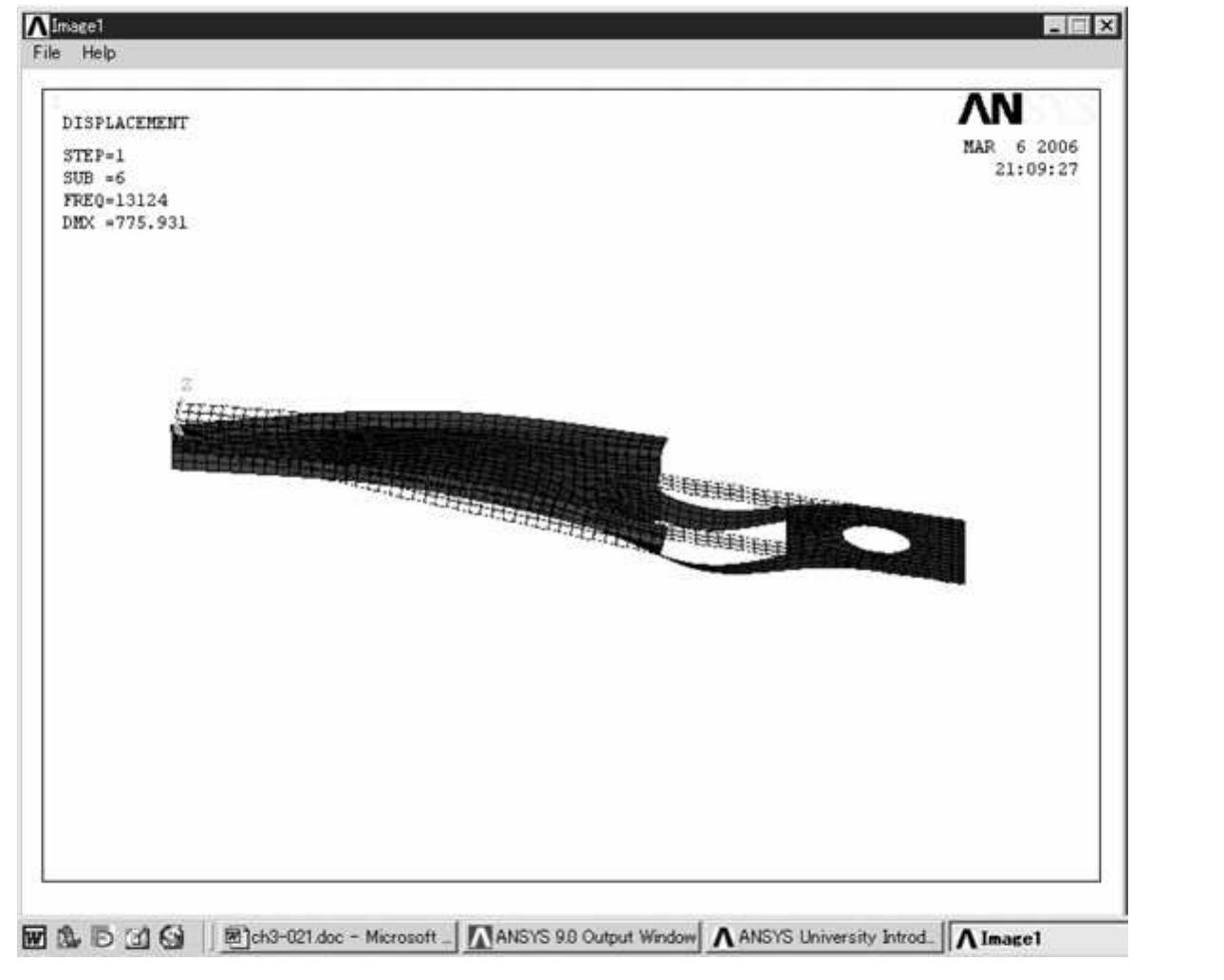














































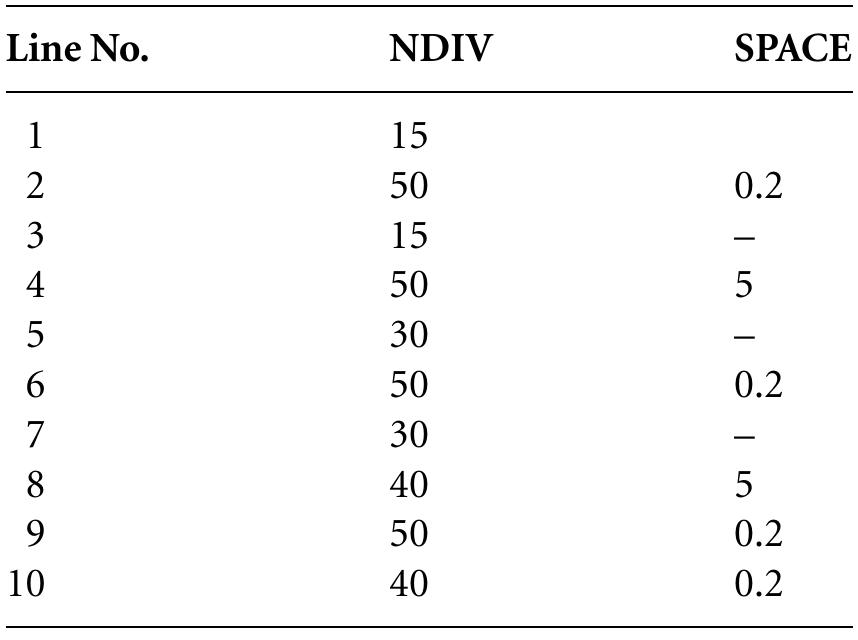

































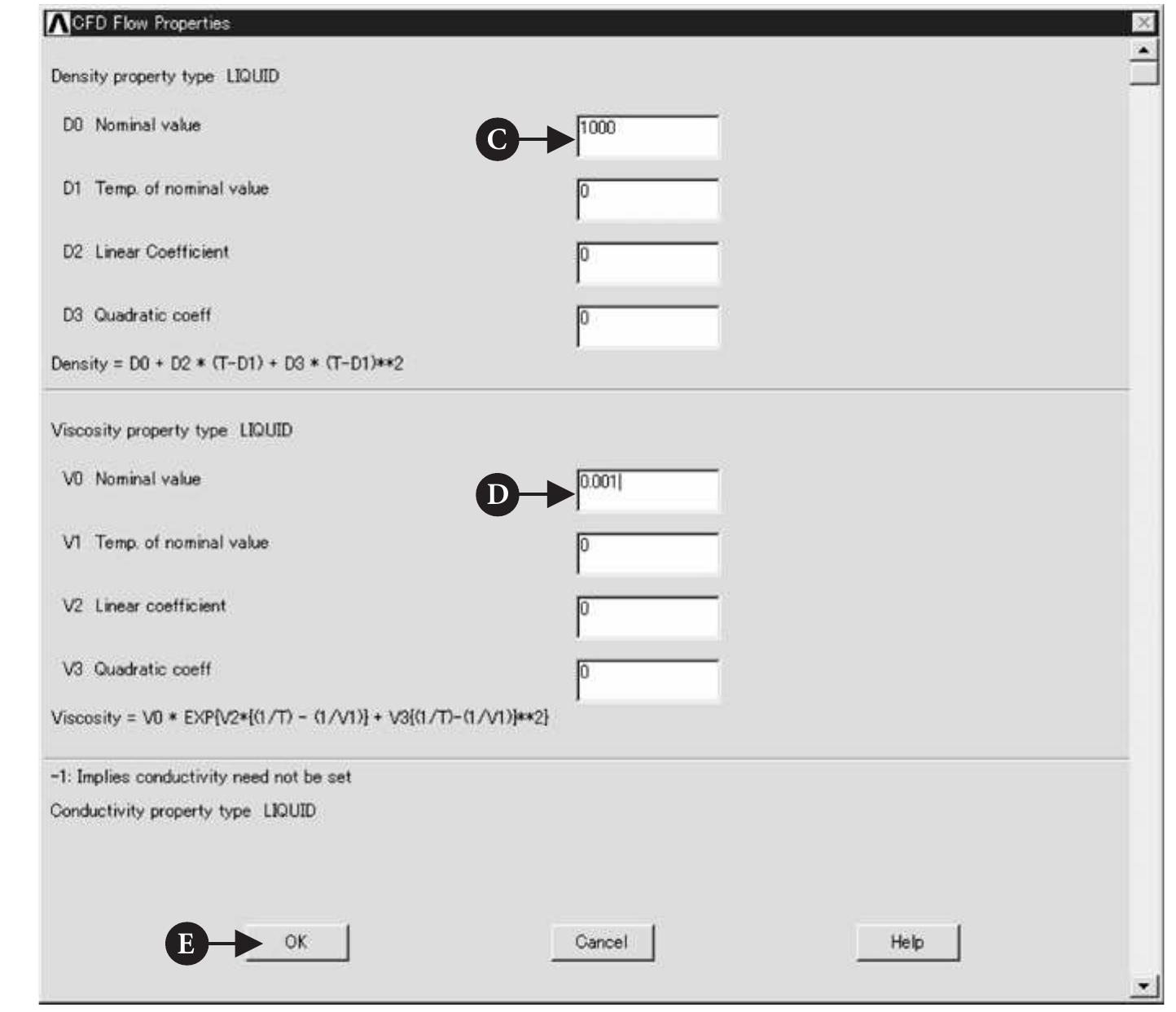

















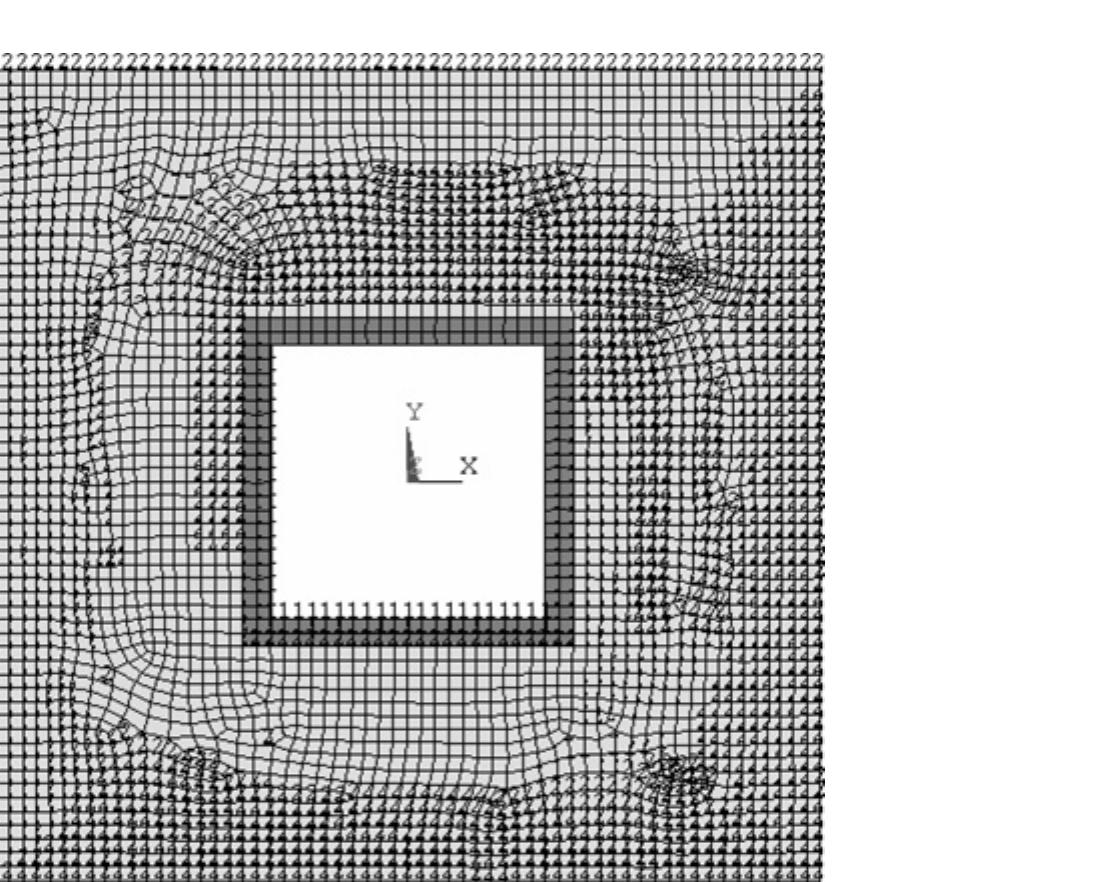
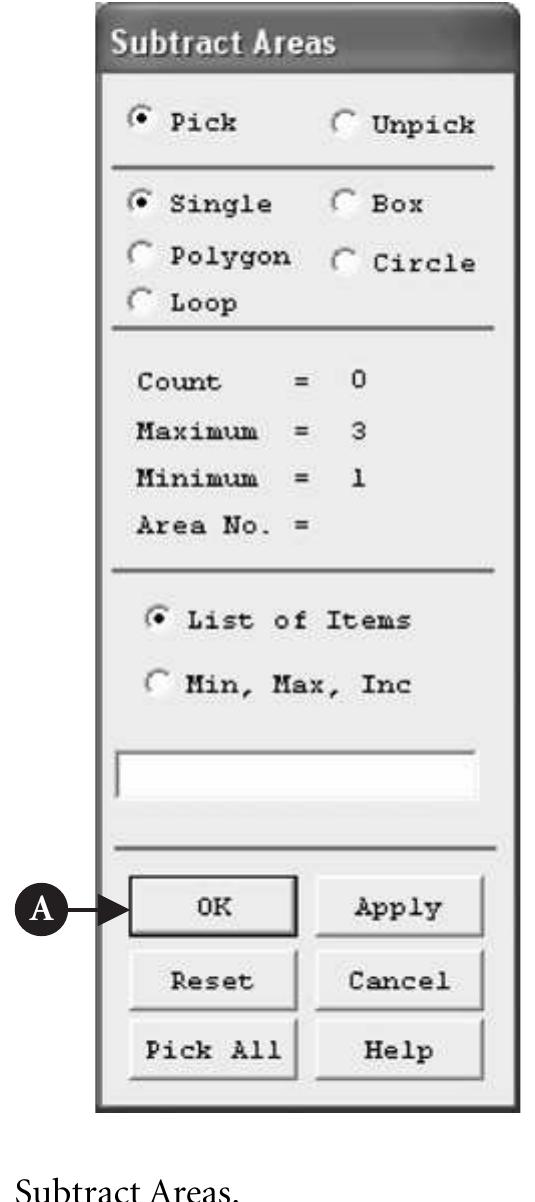
![First select the larger area (outer brick wall) and click [A] OK button in the frame
of Figure 6.11. Next, select the smaller area (inner concrete wall) and click [A] OK
button. The smaller area is subtracted from the larger area and the outer brick wall is
produced. It is shown in Figure 6.12.
Tleing an cimilar annrnarh tha innar ranrratoa urall fa panctrurtond Lream AATCVCO
which have been created. From ANSYS Main Menu select Preprocessor > Modelling](https://figures.academia-assets.com/48977193/figure_308.jpg)














































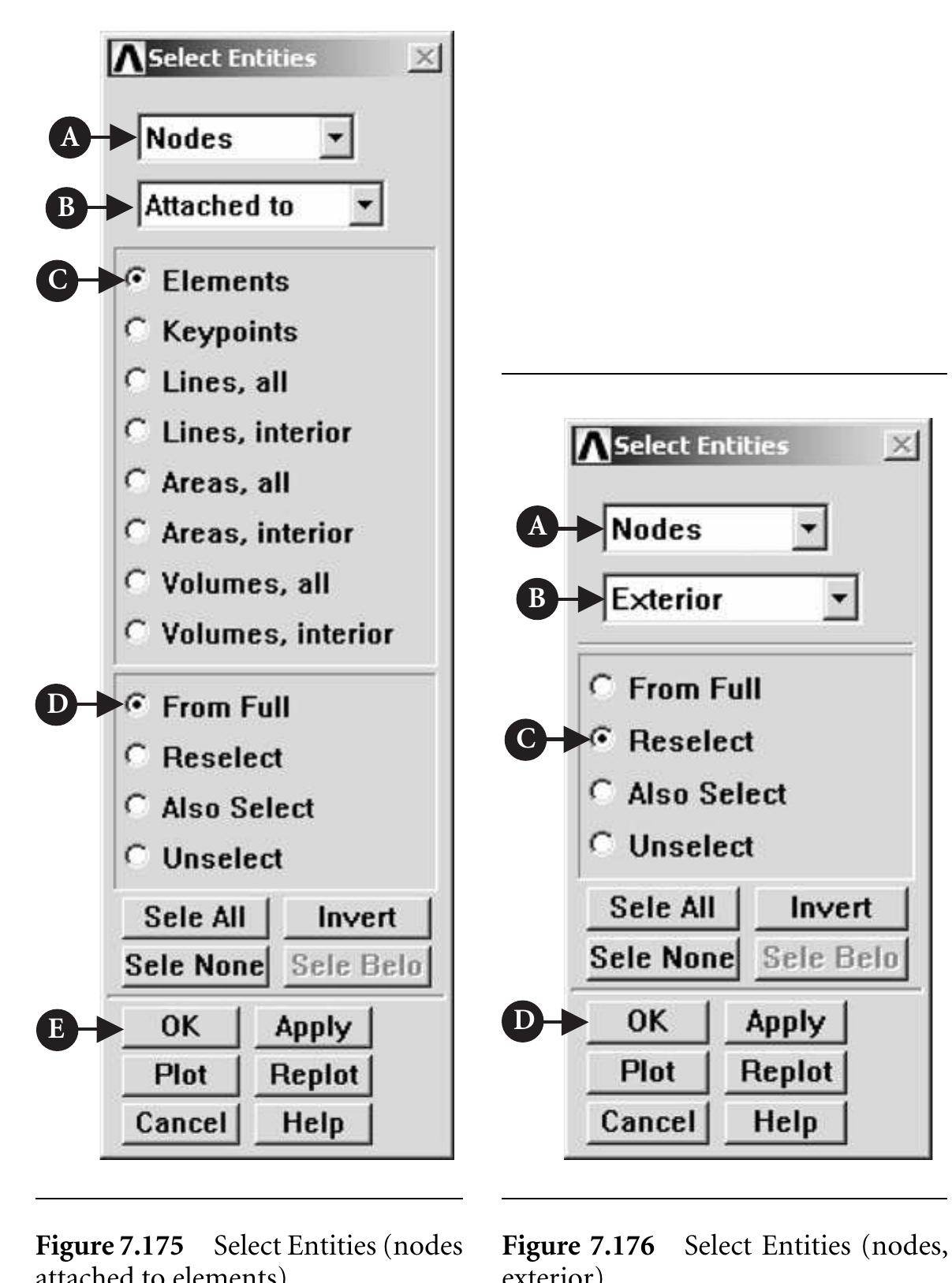
![2 eh eee ee
Activate both [A] All DOF and TEMP and input [B] TEMP value = 232°C as
shown in Figure 6.71. Finally, click [C] OK to apply temperature constraints on
nodes at the far edge of the tank. The steps outlined above should be followed to
apply constraints at nodes located at the bottom of the tank. From Utility Menu
select Select — Entities. The frame shown in Figure 6.72 appears.](https://figures.academia-assets.com/48977193/figure_355.jpg)





![Figure 6.76
select PlotCtrls — Symbols. The frame in Figure 6.77 shows the required selection:
[A] Arrows.](https://figures.academia-assets.com/48977193/figure_361.jpg)







![Figure 6.85
Results — Vector Plot — Predefined. The resulting frame is shown in Figure 6.85.
In Figure 6.85, select [A] Thermal flux TF and [B] Raster Mode. Pressing [C] OK
button implements selections and produces thermal flux as vectors. This is shown in
Figure 6.86.
6.4 HEAT DISSIPATION THROUGH RIBBED SURFACE
6.4.1 PROBLEM DESCRIPTION](https://figures.academia-assets.com/48977193/figure_367.jpg)












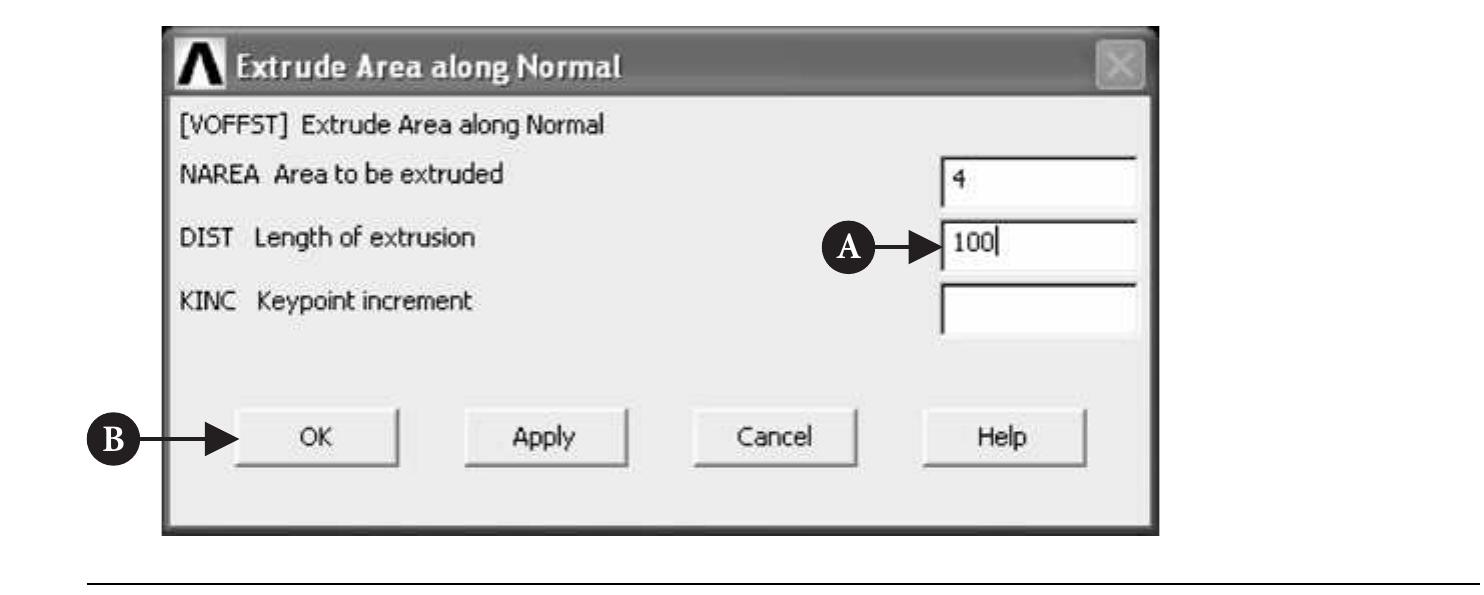



![Figure 6.105
Figure 6.105 — View of the fin with mesh network.
Select all areas of the fin except the bot-
tom area and click [A] OK button. The frame
created as a result of that action is shown in
Figure 6.107.](https://figures.academia-assets.com/48977193/figure_385.jpg)
![Clicking [A] OK button starts the solution
ArOcecc](https://figures.academia-assets.com/48977193/figure_386.jpg)











































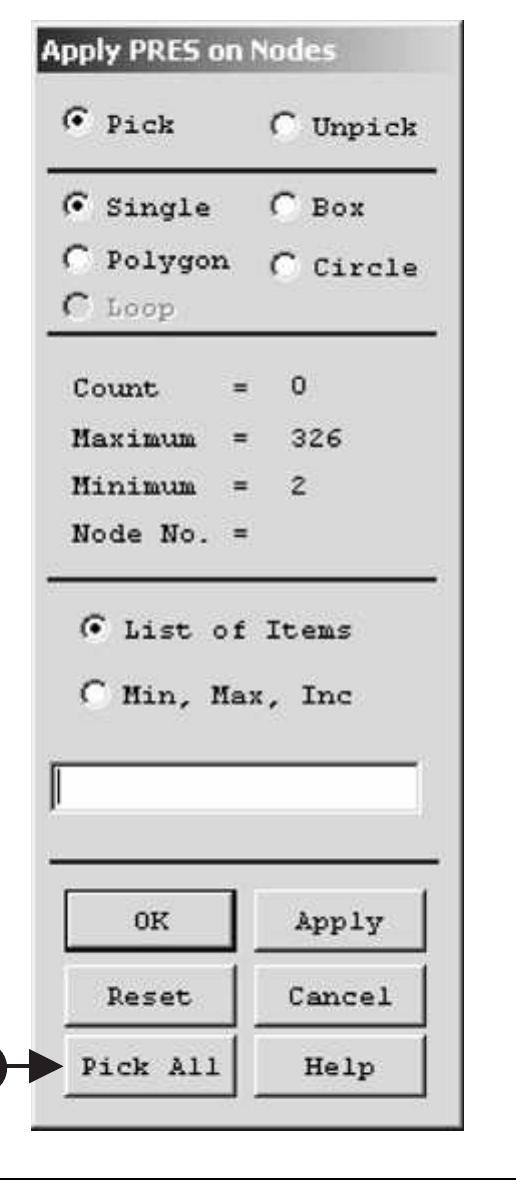
![“
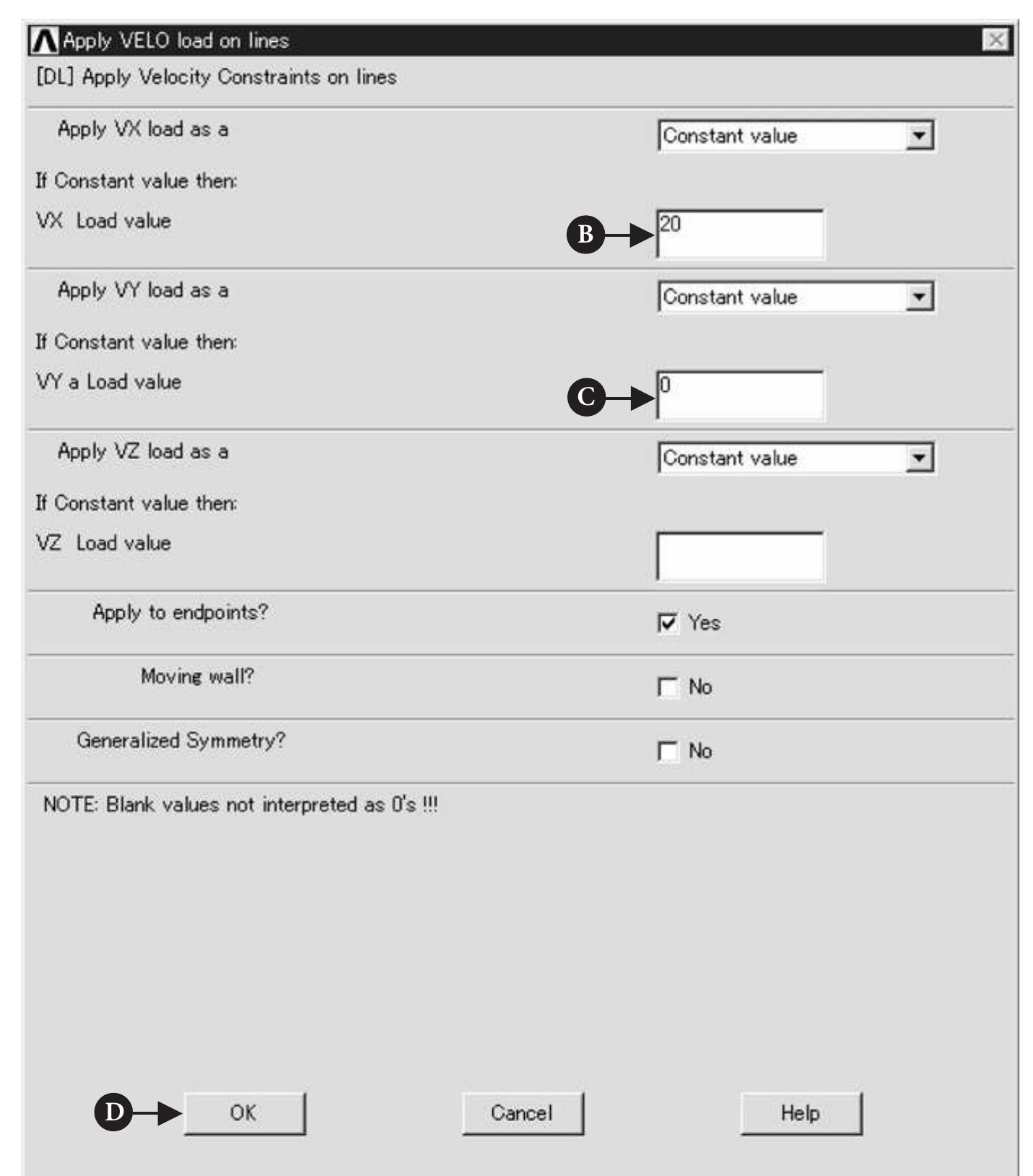
: By pressing [A] Pick All button, a frame shown in Figure 7.35 is called up.
As shown in Figure 7.35, [A] DOF to be constrained = UZ and the [
Displacement value = 2. Pressing [C] OK button applies selected constraints.
Figure 7.35](https://figures.academia-assets.com/48977193/figure_432.jpg)










































































![Pair. As a result of this selection, a frame shown in Figure 7.116 appears.
In the option [A] Facets/element edge select 2 facets/edge and click [B] OK
button as shown in Figure 7.115.](https://figures.academia-assets.com/48977193/figure_509.jpg)





































































![Figure 7.202 von Mises stress in O-ring
(deformed shape and undeformed edge).
Figure 7.203 WP Settings (Polar
system is selected).
Selections made are shown in Figure 7.206 and are implemented by clicking
A] OK.](https://figures.academia-assets.com/48977193/figure_580.jpg)







![Figure 7.215 von Mises stress due
to squeeze and external pressure
(deformed shape only).
Now, the solution stage ought to be initiated. From ANSYS Main Menu select
Solution > Solve > Current LS. The frame shown in Figure 7.198 appears together
with another frame, which gives a summary of solution options selected. After check-
ing the correctness of information, it should be closed by selecting File > Close.
Next, [A] OK should be pressed to initiate the solution.](https://figures.academia-assets.com/48977193/figure_589.jpg)

Related papers
The journal publishes original and review articles covering the concept of technical science, energy and environment, industrial engineering, quality management and other related sciences. JAES is Open-Access Journal that follows new trends and progress proven practice in listed fi elds, thus creating a unique forum for interdisciplinary or multidisciplinary dialogue. JAES is part of the electronic journal editing with a transparent editorial and review policy. Provided are:
2016
Author's declaration I declare that this submission is my own account of my research unless stated otherwise and excluding references and appendices.
All right reserved, no part of this publication may be reproduced, stored in a retrieval system or transmitted in any means, electronic, mechanical photocopying, and recording or otherwise, without permission in writing from the copyright owner.
ANSYS is one of the leading commercial finite element programs in the world and can be applied to a large number of applications in engineering. Finite element solutions are available for several engineering disciplines like statics, dynamics, heat flow, fluid flow, electromagnetics and also coupled field problems. In the present paper we summarize the current simulation capabilities of ANSYS in structural dynamics. A general classification of dynamical problems that can be solved with ANSYS is given considering not only the implicit but also the explicit solution capabilities of the code.
2016
I, the undersigned, hereby declare that the work contained in this thesis is, unless otherwise stated, my own original work and has never been submitted in part or in its entirety at any University for any requirements towards the achievement of any degree. T.T. RamOnyaqioa Stellenbosch University
This unit aims to further develop the analytical knowledge and techniques necessary to analyse and solve a variety of engineering situations and problems. • Unit abstract This unit has been designed to enable learners to use number systems, graphical and numerical methods, vectors, matrices and ordinary differential equations to analyse, model and solve realistic engineering problems. Learners will use estimation techniques and error arithmetic to establish realistic results from experiments and general laboratory work. They will then consider the conversion of number systems from one base to another and the application of the binary number system to logic circuits. Complex numbers and their application to the solution of engineering problems are also studied. Learners will look at the use of graphical techniques together with various methods of numerical integration (for example Simpson's rules) and estimation (for example Newton-Raphson). They will then go on to analyse and model engineering situations using vector geometry and matrix methods. Finally, learners will study both first and second order differential equations and their application to a variety of engineering situations dependant upon the learner's chosen discipline. On successful completion of this unit a learner will: 1 Be able to analyse and model engineering situations and solve problems using number systems 2 Be able to analyse and model engineering situations and solve problems using graphical and numerical methods 3 Be able to analyse and model engineering situations and solve problems using vector geometry and matrix methods 4 Be able to analyse and model engineering situations and solve problems using ordinary differential equations.
All rights reserved. No part of this book may be reproduced, stored in a retrieval system, or transmitted, in any form by any means, electronic, mechanical, magnetic, optical, chemical, manual, photocopying, recording or otherwise, without the prior written consent of its writer.
This a series that will include handbooks, textbooks, and professional reference books on cutting-edge areas of engineering. Also included in this series will be singleauthored professional books on state-of-the-art techniques and methods in engineering. Its objective is to meet the needs of academic, industrial, and governmental engineers, as well as provide instructional material for teaching at both the undergraduate and graduate level.
These materials may be freely distributed for non-commercial purposes under creative commons license English: http://creativecommons.org/licenses/by-nc-sa/3.0/ 한글: http://creativecommons.org/licenses/by-nc-sa/3.0/deed.ko If any changes are made to the materials they must also be freely available under this "share alike" license.
2016
This is the author’s final version of the work, as accepted for publication following peer review but without the publishers ’ layout or pagination. It is posted here for your personal use. No further distribution is permitted.
This paper discusses the different features of ANSYS and LS-DYNA in solving structural analysis using finite element approach. ANSYS and LS-DYNA are two popular engineering software tools that are used for finite element analysis. The difference between ANSYS and LS-DYNA lies in different solution procedures and time integration methods they use. ANSYS is an implicit analysis program while LS-DYNA is an explicit analysis program. This paper compares the general properties of the two programs through an impact problem and explains the reason. A simple two degrees of freedom system is solved to show how the implicit and explicit methods are implemented. Conclusively, advantages and limitations of both programs are discussed as well as their applicable areas.
All rights reserved. This is a special issue published in version 1.0 of "Global Journal of Researches in Engineering." By Global Journals Inc. All articles are open access articles distributed under "Global Journal of Researches in Engineering" Reading License, which permits restricted use. Entire contents are copyright by of "Global Journal of Researches in Engineering" unless otherwise noted on specific articles. No part of this publication may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopy, recording, or any information storage and retrieval system, without written permission. The opinions and statements made in this book are those of the authors concerned. Ultraculture has not verified and neither confirms nor denies any of the foregoing and no warranty or fitness is implied. Engage with the contents herein at your own risk. The use of this journal, and the terms and conditions for our providing information, is governed by our Disclaimer, Terms and Conditions and Privacy Policy given on our By referring / using / reading / any type of association / referencing this journal, this signifies and you acknowledge that you have read them and that you accept and will be bound by the terms thereof. All information, journals, this journal, activities undertaken, materials, services and our website, terms and conditions, privacy policy, and this journal is subject to change anytime without any prior notice.
2001
This paper describes substantial improvements in analysis capabilities in a large scale commercial finite element program made possible by the implementation of solver technology. The ANSYS program is a commercial finite element analysis program, which has been in use for thirty years. The original code, developed around a direct frontal solver has been expanded over the years to include full featured pre-and post-processing capabilities, which support a comprehensive list of analysis capabilities including linear static analysis, multiple nonlinear analyses, modal analysis and many other analysis types. The finite element models on which these analyses are used have continued to grow in size and complexity. This growth in size and complexity has been both enabled by and dependent on new solver technology along with increased computer memory and CPU resources. Beginning in 1994, ANSYS added a Jacobi preconditioned conjugate gradient solver (JCG) and subsequently an Incomplete Cholesky Preconditioned Conjugate Gradient solver (ICCG) to improve thermal analysis capabilities. In recent years the addition of the Boeing sparse matrix library for modal and static analysis, and a proprietary preconditioned conjugate gradient solver as well as additional iterative solvers, to support new CFD capabilities have greatly increased the number of solver options available in ANSYS. Most recently, in version 5.7, ANSYS has added a new domain decomposition solver for solving very large structural analysis solutions on distributed MPI-based computer systems and the newest iterative solver option, an algebraic multi-grid iterative solver (AMG). This paper will describe implementation considerations for the addition of new solver technology to a large legacy code, compare resource requirements for the various solver choices and present some comparative results from several customer generated problems. The AMG solver benefits, both in improved robustness and parallel processing efficiency, will be described. The paper will also discuss some of the implementation challenges that have been overcome to add new solver technology to a large existing code. The role of solver technology in meeting current and future demands of large scale commercial analysis codes will be discussed. 107 2. Motivation for solver improvements. The changes to ANSYS equation solvers have been motivated by several factors, which often compete for attention. Larger memory in computer systems coupled with greatly improved automatic meshing capabilities has increased the detail and size of finite element models routinely analyzed in recent years. These models lead to linear systems of equations that are now typically over 100,000 degrees of freedom (DOFs). The software capability exists to generate even larger models with millions of degrees of freedom but solver limitations often limit the practicality of such large systems.
1988
NOTICE & DISCLAIMER The Institute of Paper Chemistry (IPC) has provided a high standard of professional service and has exerted its best efforts within the time and funds available for this project. The information and conclusions are advisory and are intended only for the internal use by any company who may receive this report. Each company must decide for itself the best approach to solv- I ing any problems it may have and how, or whether, this reported information should be considered in its approach. IPC does not recommend particular products, ...
MATEC Web of Conferences
The Finite Element Analysis method, is a powerful computational technique for approximate solutions to a variety of real – world engineering problems having complex domains subjected to general boundary conditions. The method itself has become an essential step in the design or modelling of a physical phenomenon in various engineering disciplines. A physical phenomenon usually occurs in a continuum of matter (solid, liquid or gas) involving several field variables. The field variables vary from point to point, thus possessing an infinite number of solutions in the domain. The basis of finite volume method relies on the decomposition of the domain into a finite number of subdomains (elements) for which the systematic approximate solution is constructed by applying the variational or weighted residual methods. In effect, finite volume method reduces the problem to that of a finite number of unknowns by dividing the domain into elements and by expressing the unknown field variable in t...
Wiley Encyclopedia of Management, 2015
I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work.

Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
 Vishwambhar Sholapur
Vishwambhar Sholapur
