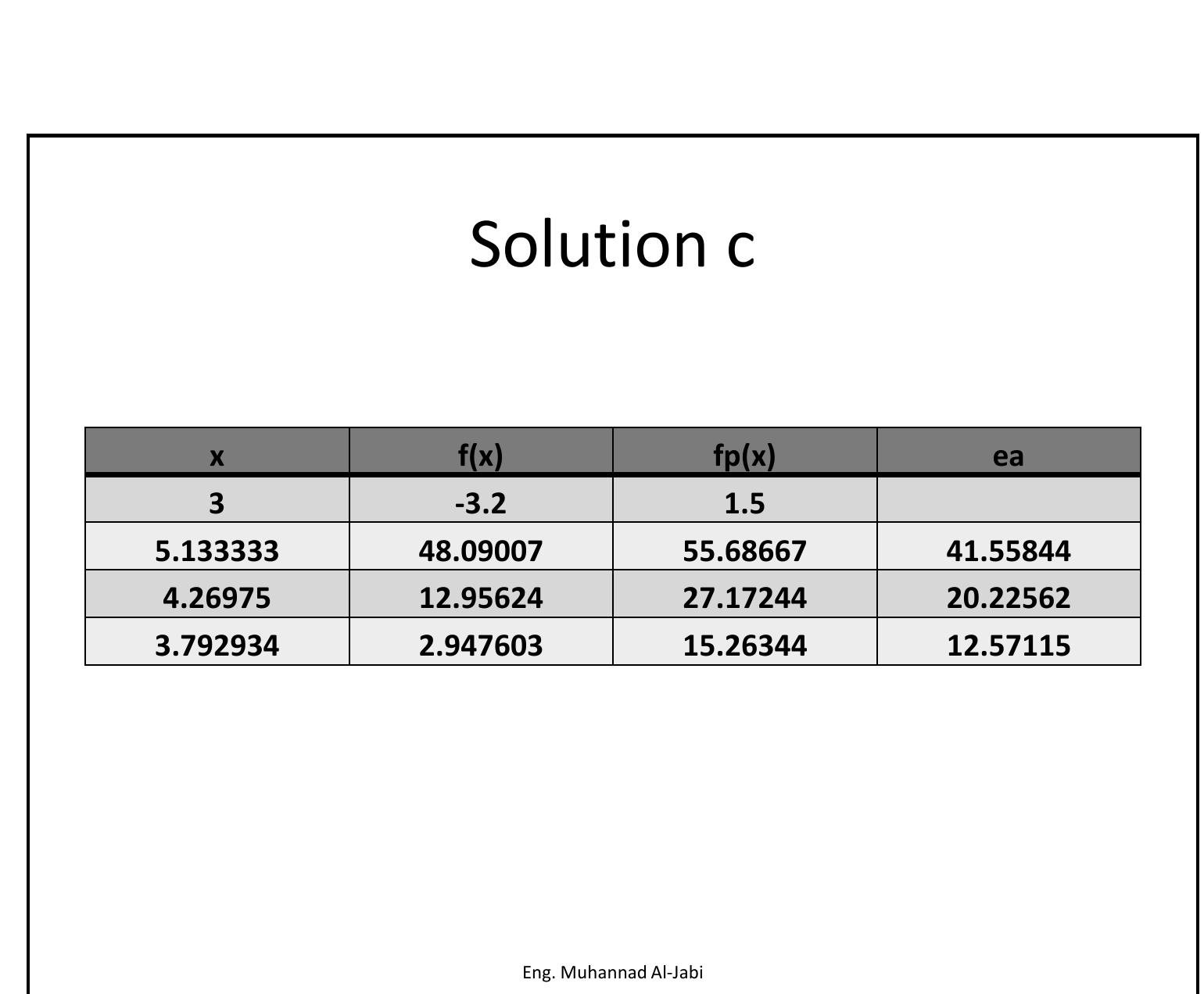
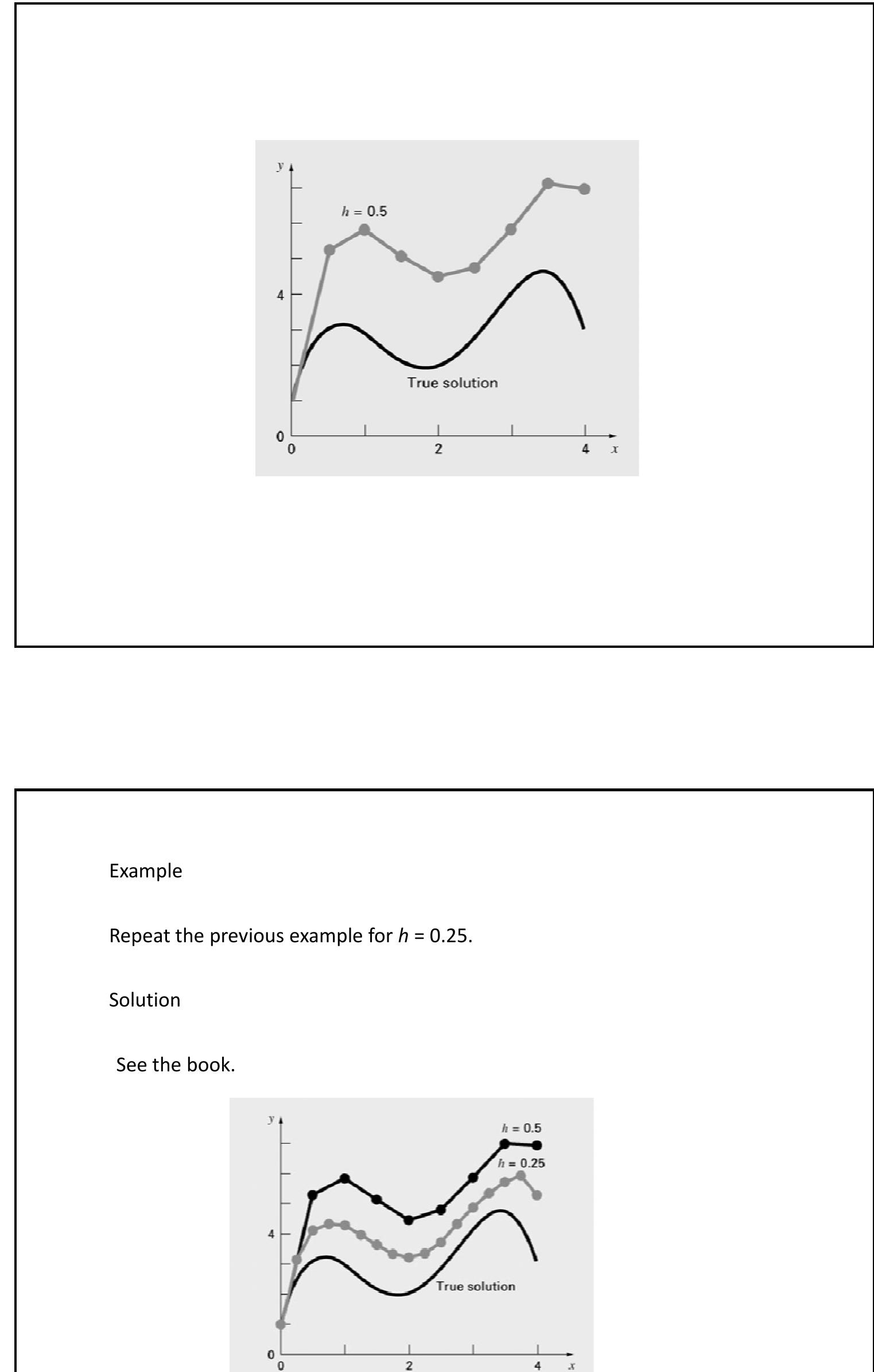
NumericalMethodsFor Engineers

International Journal for Research in Applied Science and Engineering Technology -IJRASET, 2020

The objective of this review paper is to review the concept of errors and their computation including different types of errors such as absolute error, relative error, random error, percentage error, etc. Errors play an important role in measurements or any calculations. Any measurement that we make is just an approximation, 100% accuracy is not possible. if we measure the same thing two times, there will be some variation between their values and this variation introduces an unwanted but unavoidable uncertainty in our measurements. so, here we discuss a new approach of error calculation & how to overcome from drawback of errors. Keywords: Systematic error, gross error , random error, absolute error, relative error, percentage error etc. I. INTRODUCTION Error may be classified as the difference between the measured value and the actual value. When we are measuring the values of an unknown quantity using the measuring instrument the value which we are getting is called the measured value. This measured value is different from the actual value of unknown quantity. For example, if we have done any practical measurements two times, then we get two different results both the time, there must be small error or sometimes large error between these two values. Sometimes the measured values are the same but it is an exception, the results don't need to be the same at both the time. After the measurement, the difference that occurs between the measured value and the actual value is termed as error. It is just one example but there are several examples regarding error. Errors may occur in any calculations such as mathematical, digital, technical, measurement, computational, etc. In general words, we can say that errors occur everywhere in every sector. Let's take an example, as we all know computers are one of the advanced result of our advanced technology, but even several errors occur in computational calculations. While performing experiments with industrial instruments, it is very important to operate these instruments carefully for reducing the presence of errors. Some errors are constant while some are random. We can't predict where errors occur, it occurs anywhere. Evolution of accuracy measures are used in major comparative studies of forecasting method. There are some early and most popular accuracy measures such as ROOT MEAN SQUARE ERROR (RMSE) and MEAN ABSOLUTE PERCENTAGE ERROR(MAPE). These methods are widely used for well-known issues such as higher sensitivity to outliers. When we use these accuracy measures, there must be some errors but these errors are small and seems to be good. Errors occur due to RMSE is 0.1% while errors occur due to MAPE is 1 %. A similar case can be found regarding MAPE with an error of 1.3% which seems to be good, but the error of 1.3% is larger than the average error. When we compare MAPE error concerning average error/fluctuation of stock price, MAPE error is larger than error occurred in stock price. Here poor interpretation occurs mainly due to lack of comparable benchmark used by the accuracy measures during any measurements or calculations.

International Journal for Research in Applied Science and Engineering Technology -IJRASET, 2020

The objective of this review paper is to review the concept of errors and their computation including different types of errors such as absolute error, relative error, random error, percentage error, etc. Errors play an important role in measurements or any calculations. Any measurement that we make is just an approximation, 100% accuracy is not possible. if we measure the same thing two times, there will be some variation between their values and this variation introduces an unwanted but unavoidable uncertainty in our measurements. so, here we discuss a new approach of error calculation & how to overcome from drawback of errors. Keywords: Systematic error, gross error , random error, absolute error, relative error, percentage error etc. I. INTRODUCTION Error may be classified as the difference between the measured value and the actual value. When we are measuring the values of an unknown quantity using the measuring instrument the value which we are getting is called the measured value. This measured value is different from the actual value of unknown quantity. For example, if we have done any practical measurements two times, then we get two different results both the time, there must be small error or sometimes large error between these two values. Sometimes the measured values are the same but it is an exception, the results don't need to be the same at both the time. After the measurement, the difference that occurs between the measured value and the actual value is termed as error. It is just one example but there are several examples regarding error. Errors may occur in any calculations such as mathematical, digital, technical, measurement, computational, etc. In general words, we can say that errors occur everywhere in every sector. Let's take an example, as we all know computers are one of the advanced result of our advanced technology, but even several errors occur in computational calculations. While performing experiments with industrial instruments, it is very important to operate these instruments carefully for reducing the presence of errors. Some errors are constant while some are random. We can't predict where errors occur, it occurs anywhere. Evolution of accuracy measures are used in major comparative studies of forecasting method. There are some early and most popular accuracy measures such as ROOT MEAN SQUARE ERROR (RMSE) and MEAN ABSOLUTE PERCENTAGE ERROR(MAPE). These methods are widely used for well-known issues such as higher sensitivity to outliers. When we use these accuracy measures, there must be some errors but these errors are small and seems to be good. Errors occur due to RMSE is 0.1% while errors occur due to MAPE is 1 %. A similar case can be found regarding MAPE with an error of 1.3% which seems to be good, but the error of 1.3% is larger than the average error. When we compare MAPE error concerning average error/fluctuation of stock price, MAPE error is larger than error occurred in stock price. Here poor interpretation occurs mainly due to lack of comparable benchmark used by the accuracy measures during any measurements or calculations.

ISTJ -30/1/2024

Computer operations rely heavily on numerical methods to ensure accurate and efficient results. However, despite the advancements in technology, errors may still arise due to varying factors such as hardware malfunction, software bugs, and human errors in data input. Thus, it is essential to estimate and analyze the potential errors in computer operations to maintain the integrity and reliability of the results. This paper presents an approach to estimate an error in computer operations based on numerical methods.

This section is devoted to introducing review of general information concerned with the quantification of errors such as the concept of significant digits is reviewed. Significant digits: Are important in showing the truth one has in a reported number. For example, if someone asked me what the population of my county is, I would simply respond, "The population of Adama area is 1 million!" Is it exactly one million? "I don"t know! But I am quite sure that it will not be two". The problem comes when someone else was going to give me a $100 for every citizen of the county, I would have to get an exact count in that case. That count would have been 1,079,587 in this year. So you can see that in my statement that the population is 1 million, that there is only one significant digit. i.e, 1, and in the statement that the population is 1,079,587, there are seven significant digits. That means I am quite sure about the accuracy of the number up to the seventh digit. So, how do we differentiate the number of digits correct in 1,000,000 and 1,079,587? Well for that, one may use scientific notation. For our data we can have to signify the correct number of significant digits.

Trends Journal of Sciences Research

The paper presented the results of the research related to the analysis of the reliability of computer calculations. Relevant examples of incorrect program operation were demonstrated: both quite simple and much less obvious, such as S. Rump's example. In addition to mathematical explanations, authors focused on purely software capabilities for controlling the accuracy of complex calculations. For this purpose, examples of effective use of the functionality of the decimal and fraction modules in Python 3.x were given.

International Journal of Scientific & Technology Research, 2015

From decades, the work of symbolic computations cannot be ignored in real time calculations. During the discussion of various automated machines, for estimated calculations we came to know where there are inputs and the corresponding outputs the term error is obvious. But the error can be minimized by using different suitable algorithms. This study focusses on techniques used for error correction in numeric and symbolic computations. After reviewing on different techniques discussed before we generate analysis by taking some of the parameters. The Experimental results shows that these algorithm has better performance in terms of accuracy, performance, cost, validity, safety, security, reliability and power consumption.

Journal of Complexity, 1986

The error of a numerical method may be much smaller for most instances than for the worst case. Also, two numerical methods may have the same maximal error although one of them usually is much better than the other. Such statements can be made precise by concepts from average case analysis. We give some examples where such an average case analysis seems to be more sensible than a worst case analysis.